Statistiques
Guide
"Le mot statistique désigne à la fois un ensemble de données
d'observations et l'activité qui consiste dans leur recueil, leur
traitement et leur interprétation.''
Encyclopedia Universalis
Moyenne d'une série statistique
Moyenne d'une série à valeurs individuelles
Soit la série statistique suivante qui est la liste des notes d'un
élève lors d'un trimestre de sa scolarité :
|
Notes |
15 |
10.5 |
8.5 |
12 |
14 |
10 |
12 |
11 |
16.5 |
Pour calculer la moyenne d'une série statistique à valeurs
individuelles, on fait la somme de toutes les valeurs et on divise
par le nombre de valeurs.
Ici, on a donc :
|
| = |
|
|
| = |
|
|
| = |
|
Une valeur approchée de la moyenne est de 12.17.
Exercices :
Moyenne
Moyenne d'une série à valeurs affectés d'un coefficient
Le professeur décide d'affecter un coefficient aux différentes notes
obtenues par l'élève (ou un autre élève), on a alors une nouvelle série statistique, que
l'on peut expliciter dans le tableau suivant :
| Notes | 15.5 | 9.5 | 16.5 | 15 | 10 | 16.5 |
|---|
| Coeff. | 3 | 3 | 1 | 2 | 1 | 3 |
|---|
Pour calculer la moyenne d'une série statistique à valeurs affectées
d'un coefficient, on fait le produit de chaque valeur et du
coefficient qui lui est affecté. On fait alors la somme de tous ces
produits, puis on divise par la somme des coefficients. Ici, on a
donc :
|
| = |
|
|
| = |
|
|
| = |
|
Exercices :
Moyenne avec coefficients I
Etendue
Définition :
L'étendue d'une série statistique est la différence entre la plus
grande et la plus petite des valeurs du caractère.
Dans la série statistique suivante,
| Notes | 12 | 7 | 6.5 | 11 | 10 | 17.5 | 9 | 12.5 |
|---|
l'étendue est de
17.5 - 6.5 = 11.
Exercices :
Moyenne, étendue
,
Moyenne avec coefficients II
Effectif et fréquence
Définition : On appelle
effectif
d'une valeur de caractère (ce que l'on est
en train d'étudier, dans les exemples précédents les notes d'un
élève), le nombre de fois qu'apparaît
cette valeur.
Voici une série statistique :
| Série | 2 | 0 | 1 | 0 | 3 | 2 | 3 | 3 | 0 | 0 | 0 | 0 | 4 | 4 | 3 | 6 | 3 | 6 |
|---|
et les effectifs des valeurs :
| Valeurs | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|
| Effectifs | 6 | 1 | 2 | 5 | 2 | 0 | 2 |
|---|
Définition : On appelle
fréquence
d'une valeur de caractère (ce que l'on est
en train d'étudier, dans les exemples précédents les notes d'un
élève), le quotient de l'effectif de cette valeur par l'effectif
total.
- La fréquence est un nombre, elle vérifie 0
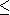
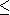 1,
et on a :
fréquence=
1,
et on a :
fréquence=
- On utilise aussi la
fréquence en pourcentage, ou pourcentage :
pourcentage=fréquence
 100 .
100 .
Dans la série statistique précédente, la fréquence de 2 est égale à
, c'est-à-dire
à peu près
0.11. La fréquence en pourcentage de 2 est
à peu près
11 % .
Exercices
Exercices :
Répartition et fréquences
,
Répartition, fréquences et regroupement
Diagrammes
Il en existe plusieurs sortes. On étudiera ceux énoncés ci-dessous :
Exercice :
Diagramme en bâton
Exemples et exercices
Télévisions
Lors d'une enquête, on a posé à 59 familles la question
suivante : "De combien de téléviseurs dispose votre foyer ?" On a
obtenu les résultats suivants :
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
L'analyse statistique de ces données permet de remplir le tableau suivant :
| Télévision |
0 |
1 |
2 |
3 |
4 |
5 |
|---|
| Effectif |
0 |
0 |
0 |
0 |
0 |
0 |
|---|
| Fréquence (%) |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
|---|
et voici l'histogramme des effectifs
Les tailles arrondies à un nombre entier de centimètres
des 70 garçons d'un club de football sont les suivantes :
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
| 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 | 160 |
L'analyse statistique de ces données permet de remplir le tableau suivant :
| Tailles |
|
|
|
|
|
|
|---|
| Effectif |
0 |
0 |
0 |
0 |
0 |
0 |
|---|
| Fréquence (%) |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
|---|
et voici l'histogramme des effectifs
Exercices
-
Etude de taille
-
Effectifs et pourcentages
-
Statistiques et pourcentages
-
Diagrammes circulaires et pourcentages
-
Angles et pourcentages
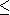
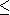 1,
et on a :
1,
et on a :
 100 .
100 .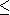
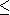 1,
et on a :
1,
et on a :
 100 .
100 .