Trigonometria a 4t ESO
Trigonometria

Pots començar amb aquesta Introducció històrica .
Preparat? Vinga, doncs: Trigonometria !!!!!!!!!!!!!!!
Introducció històrica
Measurement of the Earth's circumference
On the Sizes and Distances (Aristarchus)
El metro, el meridiano de París y Barcelona
Ingeniería Romana. Cap.1 Acueductos . Especialment els 13 minuts inicials.
Trigonometria
- Angles
- Mesurar angles en graus
- Mesurar angles en radians
- Equivalència entre graus i radians
- Mesura principal d'un angle
- Raons trigonomètriques d'un angle agut
- Resolució de triangles rectangles
- Raons trigonomètriques d'un angle qualsevol
- Relació entre les raons trigonomètriques d'angles complementaris
- Relacions entre les raons trigonomètriques d'un mateix angle
Mesurar angles en graus
Pots veure a continuació alguns angles en posició estàndard mesurats en graus:
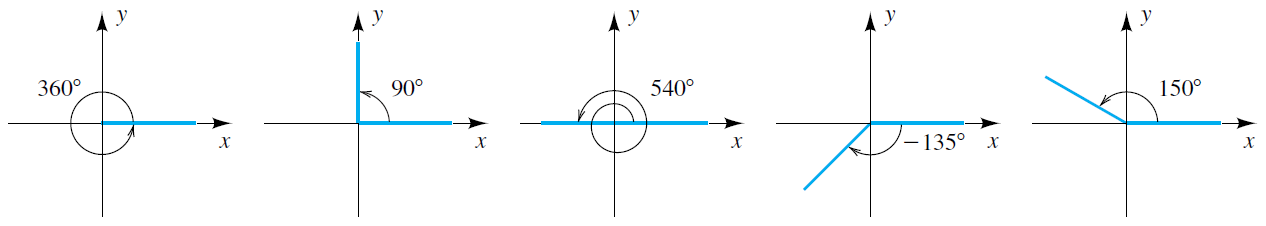
Pots modificar el valor de l'angle i veure'l en posició estàndard.
Exercicis:
- Has d'encertar l'angle dibuixat 1
- Has d'encertar l'angle dibuixat 2
Mesurar angles en radians
Si fem coincidir el vèrtex d'un angle amb el centre d'una circumferència, l'angle determina en la circumferència un arc.
|
DEFINICIÓ
Un angle d'un radian és un angle que intercepta en una circumferència un arc que té la mateixa longitud que el radi amb el que s'ha traçat. |
|
| rad |
|
|
La longitud
d'una circumferència és
. És a dir, l'arc corresponent a un angle complet fa
, això és,
vegades el radi. Per tant, l'angle complet té
una mesura de
rad. Com que , una circumferència sencera conté més de 6 vegades la longitud del radi. |
D'aquesta manera, la relació que hi ha entre un angle en radians i la longitud de l'arc associat ve donada per:
És a dir, la longitud d'un arc de circumferència és igual a l'angle mesurat en radians multiplicat per la longitud del radi.
Les tres versions d'aquesta fórmula.
| longitud de l'arc | mesura en radians de l'angle | radi de la circumferència |
Aquí pots veure la mesura en radians d'alguns dels angles més habituals.
Ves modificant els valors del radi i de la longitud de l'arc i observa com va canviant el valor de l'angle.
Exercicis:
- Angle i arc
- Angle en graus d'un arc
- El radian
- Angle en radians d'un arc
- Angle en radians i arc
- Angle en radians i arc 2
Equivalència entre graus i radians
Qualsevol fracció o múltiple d'aquesta equivalència també ho serà. Per tant:
| rad | fent la meitat de l'anterior |
| rad | fent un terç de l'anterior |
| rad | fent el doble de l'anterior |
Altres vegades caldrà donar valors aproximats:
rad,
rad.
En general, per passar de graus a radians pots multiplicar per
i per fer-ho de radians a graus per
.
Exercicis:
- Passar de graus sexagesimals a radians 1
- Passar de graus sexagesimals a radians 2
- Passar de radians a graus sexagesimals 1
- Passar de radians a graus sexagesimals 2
Mesura principal d'un angle
Mirant els angles com a girs també té sentit parlar d'angles de més de . Un angle de entenem que vol dir que s'ha girat una volta sencera i de la volta següent.
L'angle de
queda en la mateixa posició que el de
, el de
que el de
i el de
que el de
. Fer aquestes equivalències és el que en diem reduir un angle al
primer gir o trobar la mesura principal de l'angle. És a dir, donat un angle es tracta de trobar-ne un altre de positiu i menor de
que tingui el mateix costat final.
Cal fer una divisió entera per
per conèixer el quocient enter (seran les voltes senceres) i el residu (l'angle reduït al primer gir). Si l'angle és negatiu has de fer alguna cosa més.
Exercici:
- Trobar la mesura principal d'un angle
Raons trigonomètriques d'un angle agut
Exercicis:
- Raons trigonomètriques d'un angle agut
- Raons trigonomètriques de l'angle de \(45^\circ)
- Raons trigonomètriques dels angles de \(30^\circ) i \(60^\circ)
- Trobar amb calculadora les raons trigonomètriques d'un angle agut
- Trobar amb calculadora l'angle agut
Resolució de triangles rectangles
Les eines que disposem per resoldre qualsevol triangle rectangle són les següents:
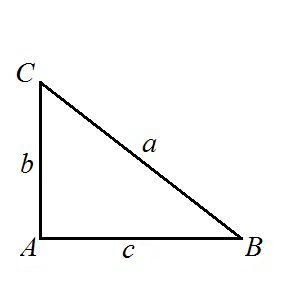
|
Teorema de Pitàgores:
Els angles aguts sumen : Les raons trigonomètriques dels angles aguts:
|
Exercicis:
- Resolució de triangles rectangles 1
- Resolució de triangles rectangles 2
- Resolució de triangles rectangles 3
- Resolució de triangles rectangles 4
- Triangle isòsceles
- Angle d'elevació
- Altura d'un arbre
- Helicòpter
- Disseny d'un robot 1
- Disseny d'un robot 2
Raons trigonomètriques d'un angle qualsevol
Altres raons trigonomètriques
Les anteriors són les raons trigonomètriques més importants, però n'hi ha d'altres que també cal conèixer, són la cotangent, la secant i la cosecant.
Es defineixen així:
Fixa't que la cosecant es pot expressar de dues formes diferents: o .
Exercicis:
- Sinus i cosinus d'un angle qualsevol
- Dibuixar angle 1
- Trobar amb calculadora les raons trigonomètriques d'un angle
- Trobar amb calculadora els angles
Relació entre les raons trigonomètriques d'angles complementaris
Exercici:
- Relació entre les raons trigonomètriques d'angles complementaris
Relacions entre les raons trigonomètriques d'un mateix angle
Hi ha altres relacions anomenades Relacions Pitagòriques. Aplicant el Teorema de Pitàgores a cadascun dels triangles rectangle següents, tenim:
|
|
Relació fonamental de la Trigonometria
|
|
|
|
|
|
|
- Angles
- Mesurar angles en graus
- Mesurar angles en radians
- Equivalència entre graus i radians
- Mesura principal d'un angle
- Raons trigonomètriques d'un angle agut
- Resolució de triangles rectangles
- Raons trigonomètriques d'un angle qualsevol
- Relació entre les raons trigonomètriques d'angles complementaris
- Relacions entre les raons trigonomètriques d'un mateix angle