Polinomis
....................................................................................................................................
- Monomis
- Polinomis en una indeterminada
- Operacions amb polinomis
- Teorema del residu
- Arrels d'un polinomi. Factorització
- MCD i mcm
- Fraccions algèbriques
- Autoavaluació
Monomis
Un monomi és una expressió algebraica formada per la multiplicació d'un nombre i una o vàries lletres:
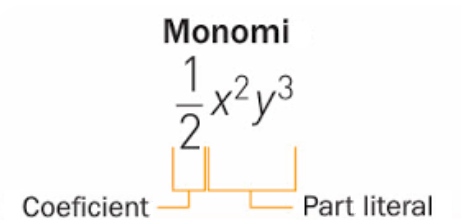
Parts d'un monomi:
- Coeficient: el coeficient és el nombre del monomi.
- Part Literal: la part literal la formen les lletres amb els seus exponents.
- Grau: el grau del monomi és la suma dels exponents de lletres que formen la part literal.
Exemple:
| Monomi | Coeficient | Part literal | Grau |
|---|---|---|---|
Operacions amb monomis
Dos o més monomis són semblants si tenen la mateixa part literal. Per exemple, són monomis semblants
i
.
Suma i resta de monomis
Per sumar i/o restar monomis aquests han de ser semblants. Si no són semblants deixem indicades la suma i/o la resta.
A la pràctica: Per fer la suma i/o resta sumem i/o restem els coeficients dels monomis i deixem la mateixa part literal.Exemples:
Multiplicació de monomis
A la pràctica: Per multiplicar monomis multipliquem el coeficient entre ells i les parts literals entre elles (important recordar les operacions amb potències).
Exemples:
Divisió de monomis:
A la pràctica: Per dividir monomis dividim els coeficients entre ells i les parts literals entre elles (important recordar les operacions amb potències).
Exemples:
Polinomis en una indeterminada
Un binomi és la suma de dos monomis que no són semblants, per exemple .
Un trinomi és la suma de tres monomis que no són semblants, per exemple .
Anomenem polinomi tota expressió que resulta de sumar un conjunt de monomis que no són semblants. Per exemple:
Anomenem grau d'un polinomi el més gran dels graus de cadascun dels seus monomis.
Anomenem terme independent d'un polinomi el monomi de grau zero. El número 0 considerat com a polinomi, diem (per conveni) que no té grau.
Exemple: és un polinomi de 5è grau i de terme independent 7.
Els polinomis els escriurem ordenadament pels graus dels monomis (de major a menor). Així, tot polinomi és de
la forma:
on és un nombre natural, i són nombres reals que anomenem coeficients.
Valor numèric d'un polinomi
El valor numèric d'un polinomi per a , que representem per , és el nombre que resulta de substituir la indeterminada pel nombre i efectuar les operacions indicades a l'expressió del polinomi
Per exemple, donat el polinomi , el valor numèric del polinomi per a el representem per i el calculem de la forma següent:
Identitat de polinomis
Dos polinomis de la mateixa indeterminada són idèntics si tenen iguals els coeficients del mateix grau.
Exercicis
Exercici 2: Escriu un polinomi que sigui:
- De tercer grau i amb dos termes
- De quart grau i amb 5 termes
- De segon grau i amb un terme
- Hi ha algun polinomi de tercer grau amb cinc termes? Per què?
Exercici 3: Indica quines de les següents expressions algèbriques no són polinomis. Justifica les respostes.
Exercici 4: Calcula, per a , el valor numèric del polinomi
Exercici 5: Determina els coeficients , i perquè els polinomis següents siguin idèntics:
Suma
Suma
La suma de dos polinomis és un altre polinomi que obtenim sumant els termes semblants (del mateix grau) de cadascun d'aquests polinomis. El grau del polinomi resultat és igual o més petit que el més gran dels graus dels polinomis que sumem.
En la pràctica es poden col·locar en columna, de manera que en una mateixa columna hi hagi els termes semblants.
Calculem si:
Els podem disposar en columna, de la manera següent:
Però és més habitual escriure els dos polinomis, l'un a continuació de l'altre, i reduir els termes semblants que hi hagi en els dos sumands.
Propietats
Commutativa:
Associativa:
Element neutre: el polinomi que només consta del terme és l'element neutre de la suma de polinomis. Si el sumem a qualsevol altre polinomi, s'obté sempre aquest mateix polinomi. És el polinomi de grau zero i de terme independent zero, és a dir, el polinomi en què tots els coeficients són nuls:
Element simètric: l'element simètric de la suma de polinomis és el polinomi oposat, que s'obté en considerar els
oposats de tots i cadascun dels seus termes. La suma d'un polinomi amb el seu oposat és igual al polinomi zero.
L'oposat d'un polinomi
s'expressa
i es verifica
Resta
Resta
La resta de dos polinomis dóna com a resultat un altre polinomi que s'obté sumant al polinomi minuend el polinomi oposat del subtrahend:
Es tracta, en definitiva, d'efectuar la suma de dos polinomis tenint en compte que, per esbrinar l'oposat del subtrahend, n'hi ha prou a canviar el signe de cadascun dels seus termes. Vegem-ne un exemple:
Calculem si:
Els podem disposar en columna, de la manera següent:
Però, com hem dit a la suma, és més habitual escriure els dos polinomis, l'un a continuació de l'altre, i reduir els termes semblants que hi hagi en els dos sumands.
Exemples 1:
Producte
Multiplicació
La multiplicació de dos polinomis és un altre polinomi de grau igual a la suma dels graus dels factors. El polinomi producte s'obté en multiplicar cada terme d'un factor per cadascun dels termes de l'altre. És a dir, s'hi ha d'aplicar successivament la propietat distributiva de la multiplicació respecte de la suma.
Cal tenir en compte que es multipliquen potències de la mateixa base i, per tant, el producte és una altra potència, l'exponent de la qual és igual a la suma dels exponents dels factors.
El producte d'un polinomi per un nombre real s'obté en multiplicar cadascun dels termes del polinomi per aquest nombre. Per exemple:
Exemples 2:
Si i , per calcular és aconsellable fer ho de la manera següent:
Propietats
Commutativa:
Associativa:
Element neutre: el polinomi és l'element neutre de la multiplicació de polinomis.
Distributiva del producete respecte la suma:
Potència
Potenciació de polinomis
Per calcular el resultat de la potencia en què és un nombre natural, multipliquem el polinomi per si mateix tantes vegades com indica l'exponent.
Per exemple:
Fixa't que el grau del polinomi és 3 , que s'obté multiplicant el grau del polinomi que és per l'exponent de la potència, que és .
En general, el grau de la potència d'un polinomi és igual al grau del polinomi multiplicat per l'exponent de la potencia.
Exercicis
Exercici 1 Considera els polinomis:
Calcula:
- Per què el grau del polinomi no és 3 ?
- Quin és el grau del polinomi ?
- Per què el grau del polinomi és 6 ?
- És cert que ?
Contesta les qüestions següents i justifica les respostes:
Exercici 2 Amb els següents polinomis, determina:
- El polinomi que verifica .
- El polinomi que verifica .
- La relació que hi ha entre els polinomis i .
Divisió de polinomis
Divisió d'un polinomi entre un monomi
En la divisió d'un polinomi entre un monomi es divideix cadascun dels monomis que formen el polinomi entre el monomi:
Exemples:
Divisió de polinomis
Efectuar la divisió P(x) : D(x) consisteix en trobar dos polinomis Q(x) i R(x) que verifiquin la igualtat:P(x) = D(x) · Q(x) + R(x)
Observa que es tracta de la propietat fonamental de qualsevol divisió. A més, els polinomis Q(x) i R(x) han de complir:
grau Q(x) = grau P(x) - grau D(x)
grau R(x) < grau D(x)
recorda que
- P(x) és el polinomi dividend
- D(x) és el polinomi divisor
- Q(x) és el polinomi quocient
- R(x) és el polinomi residu
Exemple:
A continuació, observa com es divideixen els polinomis següents:
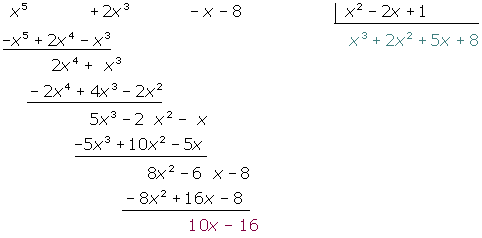
Exemple:
Ara aquests altres:
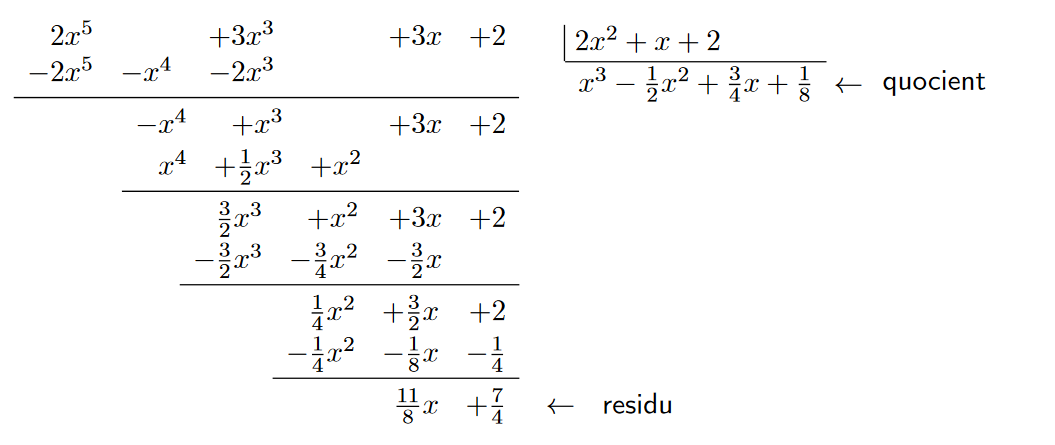
Exercici:
Donats els polinomis i , calcula
Solució: i
Regla de Ruffini
Si el divisor és un polinomi de primer grau del tipus , la divisió es pot fer de manera més senzilla aplicant una estratègia coneguda amb el nom de Regla de Ruffini.
Exemple:
Exercicis
Exercici 1 Fes la divisió . Comprova que es verifica la propietat fonamental.
Exercici 2 Efectua aquestes divisions. Aplica-hi la regla de Ruffini quan sigui possible.
Exercici 3 En una divisió, el divisor és el polinomi el quocient és i el residu és . Quin és el grau del dividend? Pots calcular-lo? Fes-ho.
Exercici 4 Determina els valors de i , de manera que, quan dividim per el residu sigui .
Exercici 5 En una divisió exacta, el dividend és i el quocient, . Calcula'n el divisor.
Exercici 6 Determina el valor de per tal que la divisió sigui exacta.
Teorema del residu
Doncs, no. No és casualitat. Això passarà en qualsevol divisió d'un polinomi per . És un fet important i és per això que s'anomena Teorema del residu.
El valor numèric d'un polinomi per , és a dir , coincideix amb el residu de la divisió d'aquest polinomi per .
Vegem per què passa això:
En dividir un polinomi qualsevol per obtindrem un quocient, que anomenem , i un residu, que anomenem R. Com a qualsevol divisió es complirà:
Si calculem utilitzant aquesta expressió del polinomi , tenim:
Això que acabem de fer és la demostració del teorema del residu.
Com que valor numèric i residu coincideixen, podem esbrinar una cosa calculant l'altra, si ens és més còmode, i viceversa.
Exemple 1: Calcula el valor numèric del polinomi per a
Hem dit que el teorema del residu ens diu que coincideix amb el residu de la divisió de entre . Llavors tenim dues opcions: calcular el valor numèric directament o fer la divisió per obtenir-ne el residu. Es tracta de veure quina és l'opció més senzilla de calcular.
- Esbrinem el valor numèric substituint la
per
en el polinomi
:
Fins i tot amb calculadora, els càlculs són una mica llargs. - També podem fer la divisió
. Podem fer-la amb la regla de Ruffini perquè el divisor és de la forma
Amb Ruffini, els càlculs són més senzills. En aquest cas, és més còmode esbrinar fent la divisió , obtenir el residu i així, .
Exemple 2: Esbrina si la divisió és exacta?
Per tal de saber si la divisió és exacta cal saber el residu. Si el residu és la divisió és exacta, si no, no ho és.
Però, en aquest cas, fer la divisió és molt llarg, podem, doncs, trobar el residu fent el valor numèric.
Considerem el polinomi que és el dividend, llavors el residu de la divisió coincideix amb :
Així que la divisió no és exacta.
Criteri de divisibilitat d'un polinomi per
Utilitzant el teorema del residu, podem afirmar que:
Un polinomi és divisible entre si, i només si, .
Exemple 3: Comprova que és divisible entre .
Podriem fer la divisió per esbrinar si el residu és zero, però en aquest cas és més senzill calcular el valor numèric de per a :
Aquest resultat ens permet assegurar que és divisible per .
Dir que és divisible per és equivalent a dir que és múltiple de i també a dir que és un divisor de .
Exercicis
Exercici 1: Tria el mètode que consideris més convenient per esbrinar el valor numèric d'aquests polinomis per al valor que s'indica:
- per a
- per a
- per a
Exercici 2: Calcula el residu de la divisió . Fes-ho mitjançant els dos procediments que hem analitzat. Explica quin és el més ràpid.
Exercici 3: Determina el valor de per tal que la divisió:
sigui exacta.
Exercici 4: Esbrina el residu de la divisió . Pots obtenir-lo sense necessitat de fer la divisió.
Exercici 5: Comprova que és divisible per . Expressa el polinomi com a producte de dos polinomis.
Exercici 6: Esbrina el valor de perquè el polinomi sigui divisible per .
Exercici 7: Un polinomi només té els divisors i . Esbrina .
Exercici 8: Calcula perquè el polinomi sigui múltiple de .
Exercici 9: Indica si són certes o falses aquestes afirmacions:
- és divisible per
- és múltiple de
- és divisor de
- és múltiple de .
- és divisor de .
Arrels d'un polinomi. Factorització
Donats un polinomi i un , diem que és una arrel o un zero de si, i només si,
Càlcul de les arrels d'un polinomi i factorització:
Les arrels van molt lligades a la factorització d'un polinomi.
Anem a veure com es troben les arrels d'un polinomi i quina relació tenen amb la seva factorització segons diferents casos:
a) Polinomis de segon grau.
Per trobar les arrels d'un polinomi , cal plantejar l'equació que resulta d'igualar el polinomi a 0 i resoldre-la. Els valors que són solució de l'equació són les arrels del polinomi. Si l'equació només té una solució , el polinomi serà . Si l'equació té dues solucions, i , llavors el polinomi .
OBSERVACIÓ: Fixa't bé que el coeficient de la apareix a la descomposició multiplicant els factors que corresponen a les arrels.
Exemple 1: Volem factoritzar
Plantegem l'equació: i resolem (en aquest cas no cal aplicar la fórmula):
Les dues arrels són 3 i -3. El polinomi factoritzat queda:
Exemple 2: Volem factoritzar
Plantegem l'equació: i resolem: només hi ha una solució, , així que en principi el polinomi factoritzat quedaria com , però hi ha un número que multiplica , el , per tant, la factorització correcta és: .
b) Polinomis de grau superior a 2.
Pels polinomis de grau superior a 2, només queda anar provant números fins a trobar una arrel. Els candidats són els divisors del terme independent (anirem fent Ruffini fins a trobar un valor pel qual el residu és 0).
El procediment es pot fer fins que al quocient quedi un polinomi de grau 2 i, aleshores, seguir amb el procediment que hem vist a l'apartat anterior, o bé segui amb Ruffini fins a que quedi al quocient un polinomi de grau 1.
Exemple: Volem factoritzar
Plantegem la divisió per Ruffini amb com a divisor:
Això vol dir que és una arrel de i que per tant:
Seguim amb 1:
Això vol dir que és una arrel de i que per tant:
Així que ja tenim:
Aquí podríem fer servir la fórmula de l'equació de segon grau, o bé seguir amb Ruffini, per exemple amb :
Això vol dir que és una arrel de i que per tant:
Així que finalment el polinomi descompost en factors queda així:
Les arrels són: (doble), i (simples), que són els valors que fan cadascun dels factors que surten a la descomposició factorial.
A l'hora de factoritzar polinomis també podem utilitzar altres eines com ara:
- Treure factor comú.
- Utilitzar les fórmules de les identitats notables.
Exercicis
Exercici 1: Determina, si és possible, les arrels enteres d'aquests polinomis:
Exercici 2: Esbrina si és una arrel del polinomi
Exercici 3: Determina les arrels del polinomi:
Exercici 4: Determina les arrels del polinomi:
Exercici 5: Calcula les arrels del polinomi .
Exercici 6: El polinomi només té una arrel real. Per què?
Exercici 7: Donat el polinomi
Esbrina una arrel entera entre els divisors del terme independent. Determina'n totes les arrels. Factoritza'l.
Exercici 8: Factoritza aquests polinomis:
Exercici 9: Calcula les arrels d'aquests polinomis mitjançant la seva factoritzacio:
Exercici 10: Les arrels d'un polinomi de segon grau són i i el coeficient de és . Quin és aquest polinomi?
MCD i mcm
El càlcul del MCD (Màxim Comú Divisor) i del mcm (mínim comú múltiple) de polinomis segueix els mateixos criteris que en el cas dels nombres enters, si bé aquí els factors no són nombres, sinó polinomis.
El MCD d’uns polinomis és el divisor comú a tots ells amb el grau més gran que existeix, i es calcula com el producte dels factors comuns amb l’exponent més petit. Si no hi ha cap factor comú el MCD és la unitat (MCD = 1).
El mcm d’uns polinomis és el múltiple comú a tots ells amb el grau més petit que existeix, i es calcula com el producte dels factors comuns i no comuns amb l’exponent més gran.
Exemple:
Calcula el MCD i el mcm de:
Primer cal factoritzar els polinomis:
I llavors calcular el MCD i el mcm:
Exercicis
Exercici 1: Calcula el MCD i el mcm dels polinomis:
- i
- i
- i
- , i
Exercici 2: Determina el MCD i el mcm de i . Comprova que el producte dels dos polinomis que acabes d'esbrinar és igual al producte dels polinomis i .
Exercici 3: El MCD de dos polinomis i és . Quin és el seu mcm?
Fraccions algèbriques
Una fracció algèbrica és una expressió de la forma
on i són polinomis amb El polinomi s'anomena numerador de la fracció i el polinomi s'anomena denominador de la fracció.
Molt sovint, les fraccions algèbriques tenen valors prohibits, això vol dir que hi ha valors de la pels quals la fracció no té valor numèric. Aquests valors prohibits són els que anul·len el denominador.
Exemple: Troba els valors prohibits de la fracció algèbrica .
Resolem l'equació
Les solucions d'aquesta equació, i són els valors prohibits de la fracció algèbrica.
És això per què:
per i això no és cap nombre!
per i això no és cap nombre!
Equivalència i simplificació de fraccions algèbriques
La fracció algèbrica és equivalent a la fracció algèbrica si, i només si,
Exemple: La fracció algèbrica és equivalent a la fracció
Simplificar una fracció algèbrica consisteix en trobar una fracció algèbrica equivalent a la inicial de manera que el numerador i el denominador tinguin el mínim grau possible.
Per simplificar fraccions algèbriques fem el següent:
- Factoritzem el numerador i el denominador.
- Eliminem els factors que apareixen simultàniament al numerador i al denominador.
Exemple 1: Simplificació de la fracció algèbrica .
- Factoritzem el numerador i el denominador.
- Eliminem els factors que apareixen simultàniament al numerador i al denominador.
Exemple 2: Simplificació de la fracció algèbrica .
Exemple 3: Simplificació de la fracció algèbrica .
Producte de fraccions algèbriques
El producte de fraccions algèbriques es fa com el producte de fraccions numèriques; és a dir, numerador per numerador i denominador per denominador, però tenint present que operem amb polinomis en comptes de nombres.
Exemples:
-
Intentarem sempre donar el resultat el més simplificat possible. Per estalviar-nos feina, abans de fer els productes factoritzem tots els polinomis, tant del numerador com del denominador, i eliminem els factors que apareixen simultàniament al numerador i al denominador.
Divisió de fraccions algèbriques
La divisió de fraccions algèbriques es fa com la divisió de fraccions numèriques, però tenint present que operem amb polinomis en comptes de nombres.
Exemples:
-
Abans de fer els productes factoritzem tots els polinomis, tant del numerador com del denominador, i eliminem els factors que apareixen simultàniament al numerador i al denominador.
Sumes i restes de fraccions algèbriques
La suma i la resta de fraccions algèbriques es fa com la suma i la resta de fraccions numèriques, però tenint present que operem amb polinomis en comptes de nombres.
Exemples:
-
Com que les dues fraccions tenen el mateix denominador podem sumar-les directament
-
En aquest cas els denominadors són diferents, per tant abans de fer la suma haurem de reduir les fraccions a comú denominador.
- Calculem el mínim comú múltiple dels denominadors
- Per fer la suma, reduïm les fraccions a comú denominador.
- Calculem el mínim comú múltiple dels denominadors
-
- Calculem el mínim comú múltiple dels denominadors
- Per fer la resta, reduïm les fraccions a comú denominador.
- Calculem el mínim comú múltiple dels denominadors
-
- Calculem el mínim comú múltiple dels denominadors
- Per fer l'operació, reduïm les fraccions a comú denominador.
- Calculem el mínim comú múltiple dels denominadors
Exercicis
Exercici 1: Simplifiqueu les següents fraccions algèbriques:
Exercici 2: Efectueu les següents operacions amb fraccions algèbriques simplificant al màxim els resultats:
Exercici 3: Efectueu les següents operacions. Simplifiqueu al màxim el resultat obtingut.
Exercici 4: Per quina fracció algèbrica cal multiplicar per obtenir ?
Autoavaluació
Exercici 1: Contesta raonadament les qüestions següents:
- Si en restar dos polinomis de tercer grau obtenim un polinomi de segon grau, quina relació hi ha entre els coeficients dels termes de grau més gran dels dos polinomis?
- Un polinomi és divisible per . Quin és el valor de
- El grau d'un polinomi és . Quin és el grau de
- Si és una arrel de , quin factor esbrinarem amb tota seguretat en la descomposició factorial de ?
Exercici 2: Donats els polinomis:
calcula:
Exercici 3: Determina el valor de perque el polinomi sigui divisible per
Exercici 4: Donat el polinomi , esbrina les seves arrels i efectua'n la factorització.
Exercici 5: Factoritza els polinomis:
Simplifica la fracció algèbrica
Exercici 6: Fes les operacions següents: