Funcions a 1r de BAT

Funcions

En molts fenòmens quotidians ens trobem diverses magnituds que estan relacionades entre elles. Per exemple:

Quan anem a un aparcament de pagament, la quantitat de diners que paguem està relacionada amb (depèn de) la quantitat de temps que haguem tingut aparcat el cotxe.

El salari mensual d'un venedor pot ser que depengui del volum de vendes que hagi fet durant aquell mes.

Si organitzem un concert, la quantitat de diners que ingressarem depèn de la quantitat de gent que hi assisteixi.

L'interès obtingut invertint 1000 € durant 1 any depèn de la taxa d'interès anual.

Sovint, la relació entre aquestes magnituds és tan forta que els valors d'una determinen els valors de l'altra. Aquestes relacions són sovint representades per expressions matemàtiques i ens porten al concepte de funció.

I, estudiant les funcions, podrem trobar quins valors d'una fan que creixi o decreixi l'altra, quin/s valor/s d'una ens porten a màxims o mínims de l'altra, quins valors d'una fan que l'altra creixi o decreixi més ràpidament o més lentament, ... qüestions totes elles molt interessants en moltes branques de la ciència i la societat.

Preparat? Vinga, doncs: Funcions .

Concepte de funció.

Aquestes magnituds que hem dit que estan relacionades poden ser constants o variables (prenen valors diferents). Evidentment les que ens interessa estudiar aquí són les variables, perquè en tant que varien podem trobar quin valor d'una fa que l'altra assoleixi un valor determinat, quin valor d'una fa que l'altra assoleixi un valor màxim, etc.

EXEMPLE

Quan anem amb un vehicle a una estació de servei a posar combustible (per exemple, gasoil, a 1.129 €/l) ens pot interessar estudiar la relació que hi ha entre les variables: preu que paguem i quantitat de combustible que posem. Hem de fixar-nos que aquestes dues variables no juguen el mateix paper en aquesta relació. Si l'estació és d'autoservei i disposa d'una màquina on dius quina quantitat de diners vols posar, la quantitat de combustible depèn de la quantitat de diners que diguis. És a dir, en aquesta situació diríem que:

la quantitat de diners és la variable independent
la quantitat de combustible és la variable dependent

Mentre que si a la màquina li hem de dir la quantitat de combustible que volem posar, llavors el preu que hem de pagar depèn de la quantitat de combustible que hem decidit posar. Diríem que, ara, en aquesta nova situació:

la quantitat de combustible és la variable independent
la quantitat de diners és la variable dependent

Així que el tipus de variable (dependent o independent) no és una característica pròpia de la variable sinó del paper que hi juga en cada relació.

DEFINICIÓ

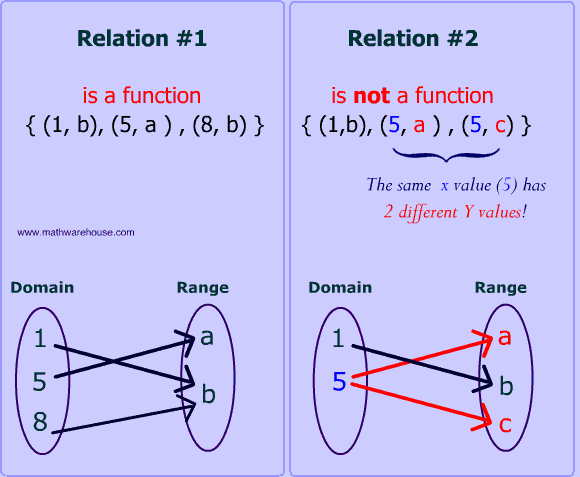
Aquesta relació de dependència entre dues variables diem que és una funció si a cada valor real de la variable independent li correspon un únic valor de la variable dependent.

Normalment anomenen $x$ la variable independent, i $y$ la variable dependent.

De fet quan diem que hi ha una relació entre les magnituds, el que passa realment és que la relació es dóna entre els valors d'aquestes magnituds, i aquests valors formen conjunts numèrics. És per això que sovint parlem de funció del conjunt $A$ al conjunt $B$ . Així, doncs, una funció la representem

$f :$	$A ⟶ B$
	$x ⟶ y = f (x)$

$f$ és el nom que li donem a la funció, $A$ és el conjunt de valors que pren la variable independent i $B$ és el conjunt que conté els valors que pren la variable dependent. El conjunt $A$ s'anomena domini de la funció, $D_{f}$ o $D (f)$ ; i el $B$ conté el recorregut, $R_{f}$ o $R (f)$ , que és el conjunt de valors que pren la variable dependent.

L'expressió $y = f (x)$ (es llegeix: $y$ és igual a efe d' $x$ ) indica que $y$ és funció de (depèn de) $x$ . Diem que $y$ és la imatge d' $x$ i que $x$ és l'antiimatge d' $y$ per la funció $f$ .

Per ajudar a entendre aquests conceptes, observa a la figura següent, la funció que relaciona el temps del dia (en hores) amb la temperatura (en ºC).

Podem dir que la imatge de 5 és 12, i ho expressem:

f (5) = 12

. Fixa't que trobar la imatge de 5, en aquesta funció, és respondre la pregunta: quina temperatura feia a les 5 h?

També, que l'antiimatge de 13 és 2, i ho expressem: $f^{- 1} (13) = 2$ , però, $f^{- 1} (15) = {3, 4}$ . Trobar antiimatges de 10, és respondre la pregunta: a quina/es hores feia una temperatura de 10 ºC?

Aquesta funció també la podem tenir definida pel conjunt de parells ordenats, en els que la primera coordenada ( $x$ ) és el valor de la variable independent i la segona coordenada ( $y$ ) és el valor de la variable dependent.

{(1, 9), (2, 13), (3, 15), (4, 15), (5, 12), (6, 10)}

RECORDA

Característiques d'una funció d'un conjunt $A$ a un conjunt $B$ .

Cada element d' $A$ ha de tenir una imatge a $B$ .
Alguns elements de $B$ poden no tenir antiimatge a $A$ .
Dos o més elements d' $A$ poden tenir la mateixa imatge a $B$ .
Un element d' $A$ no pot tenir dues o més imatges a $B$ .

Domini i recorregut d'una funció

Ja hem comentat en un apartat anterior què és el domini d'una funció agafant com a exemple la funció que relaciona el temps del dia (en hores) amb la temperatura (en ºC).

Només ens cal formalitzar-ho.

DEFINICIÓ

El conjunt de tots els valors reals de la variable independent que tenen per imatge un nombre real s'anomena domini de la funció, i l'expressem $D_{f}$ o $D (f)$ .

En altres paraules, el domini d'una funció són tots els valors de la variable independent que tenen imatge.

DEFINICIÓ

El recorregut, $R_{f}$ o $R (f)$ , és el conjunt de valors que pren la variable dependent, això és, el conjunt de totes les imatges. També s'anomena rang.

En altres paraules, el recorregut d'una funció són tots els valors de la variable dependent que tenen antiimatge, es a dir, que són imatge d'algun valor del domini.

EXEMPLE

Practica amb el següent Exercici

RECORDA

El domini fa referència a valors de la variable independent $x$ , així , en un gràfic els tenim a l'eix d'abscisses (l'horitzontal), mentre que el recorregut el formen els valors de la variable dependent $y$ , així , en un gràfic els tenim a l'eix d'ordenades (el vertical).

Practica amb el següent Exercici

Funcions algèbriques

Anomenem funcions algèbriques aquelles funcions que es poden formar amb les operacions algèbriques habituals: suma, multiplicació, divisió, i càlcul d'arrels, quadrades, cúbiques, ...

Les estudiem a continuació:

Funcions polinòmiques
Funcions racionals
Funcions irracionals

Practica amb el següent Exercici

Quan les variables que defineixen la funció corresponen a magnituds de la realitat, cal tenir en compte aquest context per determinar tant el domini com el recorregut. Fixa't en aquest exemple:

EXEMPLE

Quan es deixa caure un cos des d'una determinada altura respecte del terra, l'altura a què se situa depén del temps que transcorre des de l'inici del moviment. La relació de dependència és la que expressa la funció $h (t)$ . Analitza la situació de tot plegat i intenta entendre les expressions del domini i del recorregut.

Funcions polinòmiques

Anomenem funcions polinòmiques les que tenen com a expressió algèbrica un polinomi. Ja en coneixes unes quantes de cursos anteriors.

Funció constant
Funció lineal
Funció afí
Funció quadràtica

DEFINICIÓ

Ja hem dit que les funcions polinòmiques són les que tenen com a expressió algèbrica un polinomi:

$f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + . . . + a_{2} x^{2} + a_{1} x + a_{0}$

$n \in ℕ$ és el grau del polinomi

$a_{n}, a_{n - 1}, . . ., a_{2}, a_{1}, a_{0} \in ℝ$ són els coeficients del polinomi

El terme o monomi més important és el de màxim grau, $a_{n} x^{n}$ . D'ell depenen moltes característiques de la funció. És per això que l'anomenem terme dominant del polinomi o de la funció polinòmica.

EXEMPLE

Aquí podràs veure altres Exemples de funcions polinòmiques .

EXEMPLE

En el cas de les funcions polinòmiques les operacions que interven, sumes, productes, potències, ... les podem fer amb qualsevol nombre real i el resultat serà també un nombre real. És per això que el domini són tots els nombres reals,

D_{f} = ℝ

RECORDA

Les funcions polinòmiques tenen com a expressió algèbrica $f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + . . . + a_{2} x^{2} + a_{1} x + a_{0}$ .
Qualsevol nombre real té imatge, així que el seu domini sempre és $ℝ$ , és a dir, $D_{f} = ℝ$ .
Sempre són contínues, això vol dir que les podem dibuixar sense aixecar el llapis del paper.
Les de grau parell tenen branques infinites que van totes dues cap amunt quan el coeficient del terme dominant és positiu i totes dues cap avall quan és negatiu.
Les de grau senar tenen branques infinites que van la de l'esquerra cap avall i la de la dreta cap amunt quan el coeficient del terme dominant és positiu i a l'inrevés quan és negatiu.
Les funcions polinòmiques més elementals són les que tenen un sol monomi, $f (x) = x^{n}$ . Observa com són els gràfics d'aquestes funcions i quina influència té l'exponent.

Funció constant

DEFINICIÓ

Anomenem funcions constants les que tenen com a expressió algèbrica $f (x) = k$ , on $k \in ℝ$ . El polinomi és de grau zero.

EXEMPLE

RECORDA

Les funcions constants tenen com a expressió algèbrica $f (x) = k$ , on $k \in ℝ$ .
Qualsevol nombre real té imatge (tots tenen la mateixa imatge), així que el seu domini és $ℝ$ , és a dir, $D_{f} = ℝ$ .
Només $k$ té antiimatge/s, és a dir, $R_{f} = {k}$ .
La seva representació gràfica sempre és una recta horitzontal que passa pel punt $(0, k)$ . És per això que $k$ es diu que és l'ordenada a l'origen.

Funció lineal

DEFINICIÓ

Anomenem funcions lineals les que tenen com a expressió algèbrica $f (x) = k x$ , on $k \in ℝ, k \neq 0$ . El polinomi és de grau 1 i amb terme independent nul.

EXEMPLE

RECORDA

Les funcions lineals tenen com a expressió algèbrica $f (x) = k x$ , on $k \in ℝ, k \neq 0$ .
Qualsevol nombre real té imatge, així que el seu domini és $ℝ$ , és a dir, $D_{f} = ℝ$ .
Qualsevol nombre real té antiimatge, és a dir, $R_{f} = ℝ$ .
La seva representació gràfica sempre és una recta que passa pel punt $(0, 0)$ . El valor de $k$ és una mesura de la inclinació de la recta, és per això que s'anomena pendent.
Quan $k > 0$ la funció és creixent mentre que quan $k < 0$ la funció és decreixent.
Especialment interessant és la funció $f (x) = x$ , anomenada funció identitat i expressada amb $I (x) = x$ . El seu gràfic correspon a la bisectriu dels quadrants 1r i 3r.
També cal esmentar la funció $f (x) = - x$ . El seu gràfic correspon a la bisectriu dels quadrants 2n i 4t.

Funció afí

DEFINICIÓ

Anomenem funcions afins les que tenen com a expressió algèbrica $f (x) = m x + n$ , on $m, n \in ℝ, m, n \neq 0$ . El polinomi és de grau 1 i amb terme independent no nul.

EXEMPLE

RECORDA

Les funcions afins tenen com a expressió algèbrica $f (x) = m x + n$ , on $m, n \in ℝ, m, n \neq 0$ .
Qualsevol nombre real té imatge, així que el seu domini és , és a dir, $D_{f} = ℝ$ .
Qualsevol nombre real té antiimatge, és a dir, $R_{f} = ℝ$ .
A les funcions afins tenen un paper molt important els valors de $m$ i $n$ . És per això que reben noms especials: $m$ és el pendent i $n$ l'ordenada a l'origen. Modificant els seus valors observa quina influència tenen en els seus gràfics i el perquè dels seus noms.

Funció quadràtica

DEFINICIÓ

Anomenem funcions quadràtiques les que tenen com a expressió algèbrica $f (x) = a x^{2} + b x + c$ , on $a, b, c \in ℝ, a \neq 0$ . El polinomi és de grau 2.

EXEMPLE

RECORDA

Les funcions quadràtiques tenen com a expressió algèbrica $f (x) = a x^{2} + b x + c$ , on $a, b, c \in ℝ, a \neq 0$ .
Qualsevol nombre real té imatge, així que el seu domini és , és a dir, $D_{f} = ℝ$ .
El gràfic d'una funció quadràtica és una paràbola.
Les branques de la paràbola van totes dues cap amunt quan $a > 0$ i van totes dues cap avall quan $a < 0$ .
El punt més important del gràfic és el vèrtex $V = (v_{x}, v_{y})$ .
Les coordenades del vèrtex es poden trobar així: l'abscissa $v_{x} = \frac{- b}{2 a}$ i l'ordenada $v_{y} = f (v_{x}) = f (\frac{- b}{2 a})$ .
En $x = v_{x}$ la funció presenta un màxim quan $a < 0$ i un mínim quan $a > 0$ .
No tots els nombres reals tenen antiimatge, és a dir, $R_{f} \neq ℝ$ .
Quan $a > 0 R_{f} =$ [ $v_{y}, + ∞$ [
Quan $a < 0 R_{f} =$ ] $- ∞, v_{y}$ ]
El valor absolut de $a$ determina l'obertura de la paràbola, quan més gran és, més tancada és la paràbola i quan més petit, més oberta.

Funcions racionals

DEFINICIÓ

Les funcions racionals són les que tenen com a expressió algèbrica:

$f (x) = \frac{P (x)}{Q (x)}$

on $P (x)$ i $Q (x)$ són polinomis, i $Q (x) \neq 0$

EXEMPLE

Aquí podràs veure altres Exemples de funcions racionals .

EXEMPLE

En el cas de les funcions racionals sempre hi ha una divisió. Si per trobar la imatge d'algun nombre real cal dividir per 0 no ho podrem fer i aquest nombre no tindrà imatge i per tant no serà del domini. Hem de mirar el denominador i esbrinar quin/s valor/s fan que valgui 0. És a dir, hem de resoldre l'equació

x + 4 = 0

. La solució,

x = - 4

, no tindrà imatge,

f (- 4) = \frac{18}{0} \notin ℝ

. Tots tindran imatge excepte

- 4

. Per tant

D_{f} = ℝ \sim {- 4}

. També ho podem expressar d'aquestes altres maneres:

D_{f} = ℝ \sim {- 4} = {x \in ℝ / x \neq - 4} =

] -

, -4 [

]-4, +

[

RECORDA

Les funcions racionals tenen com a expressió algèbrica $f (x) = \frac{P (x)}{Q (x)}$ .
No sempre tenen imatge tots els nombres reals, així que el seu domini no sempre és $ℝ$ .
No sempre són contínues, això vol dir que sovint s'haurà d'aixecar el llapis del paper per dibuixar-les. Sovint tenen discontinuïtats.
Sovint tenen asímtotes. Les asímptotes són rectes (que no formen part de la funció) a les que la funció es va apropant cada vedada més.
Les funcions racionals més elementals són les que tenen l'expressió algèbrica, $f (x) = \frac{1}{x^{n}}$ . Observa quina influència té l'exponent en aquestes funcions.

Exemples de funcions racionals

EXEMPLE

1.- $f (x) = \frac{x - 1}{x + 1}$	2.- $f (x) = \frac{5 x + 3}{2 x - 4}$	3.- $f (x) = \frac{1}{x^{2} - 1}$
4.- $f (x) = \frac{x + 2}{x^{2} + 1}$	5.- $f (x) = \frac{x}{x^{2} - 1}$	6.- $f (x) = \frac{3 x - 8}{x^{2} - 9}$
7.- $f (x) = \frac{x^{2} + 1}{x - 1}$	8.- $f (x) = \frac{x^{2}}{x^{2} + 1}$	9.- $f (x) = \frac{x^{2}}{x^{2} - 1}$
10.- $f (x) = \frac{x^{2} - 1}{x + 1}$	11.- $f (x) = \frac{1 - x}{{(x + 1)}^{2}}$	12.- $f (x) = \frac{1}{x^{2} + 1}$
13.- $f (x) = \frac{4 x}{x^{2} + 4}$	14.- $f (x) = \frac{x^{2} + 1}{x^{2} - 1}$	15.- $f (x) = \frac{x^{3}}{x^{2} - 1}$
16.- $f (x) = \frac{x^{4} - 2 x^{2}}{x^{2} - 1}$	17.- $f (x) = \frac{x}{x^{2} - 5 x + 4}$	18.- $f (x) = \frac{x^{2}}{x^{2} + x - 4}$

$f (x) =$

Per veure-ho millor, pots modificar l'escala dels eixos clicant i arrossegant quan el ratolí està damunt de l'eix.

Funcions irracionals

DEFINICIÓ

Les funcions irracionals són les que en la seva expressió algèbrica apareixen arrels:

$f (x) = \sqrt[n]{x}$ , $n \in ℕ$

EXEMPLE

En aquest cas hi ha una arrel d'índex parell. Si per trobar la imatge d'algun nombre real cal fer l'arrel quadrada d'un nombre negatiu, no ho podrem fer i aquest nombre no tindrà imatge i per tant no serà del domini. Hem de mirar el radicant (el que hi ha dins de l'arrel) i esbrinar quin/s valor/s fan que sigui positiu o 0. És a dir, hem de resoldre la inequació

6 - 3 x \geq 0

. Les solucions,

x \leq 2

, són els que tenen imatge, els altres no en tenen. Per exemple

f (3) = \sqrt{6 - 3 \cdot 3} = \sqrt{- 3} \notin ℝ

. Per tant

D_{f} =

] -

, 2 [. També ho podem expressar d'aquesta altra manera:

D_{f} = {x \in ℝ / x \leq 2} =

] -

, 2 [

RECORDA

Les funcions irracionals són les que en la seva expressió algèbrica apareixen arrels: $f (x) = \sqrt[n]{x}$ , $n \in ℕ$
No sempre tenen imatge tots els nombres reals, així que el seu domini no sempre és $ℝ$ .
Les funcions irracionals més elementals són les que tenen l'expressió algèbrica, $f (x) = \sqrt[n]{x}$ . Observa quina influència té l'índex en aquestes funcions.

Funcions definides a trossos

DEFINICIÓ

Les funcions definides a trossos són les que en la seva expressió algèbrica apareixen diferents expressions, però cada expressió actua en una de les parts (trossos) del domini de la funció.

EXEMPLE

RECORDA

Les funcions definides a trossos són les que en la seva expressió algèbrica apareix una expressió diferent per a cada tros del domini de la funció.
Molt sovint no són contínues.
Una funció definda a trossos molt especial és la que associa cada nombre real $x$ amb el seu valor absolut $∣ x ∣$ i la seva expressió algèbrica es pot escriure així: $f (x) = ∣ x ∣ = {\begin{array}{ll} - x & si & x < 0 \\ x & si & x \geq 0 \end{array}$ . Observa quin és el seu gràfic.

Practica amb els següents exercicis:

Avaluar una funció 2 .
Agència de viatges 1 .

Taula de variació d'una funció

DEFINICIÓ

La taula de variació d'una funció es una taula de dues files on es recull la informació de la seva variació, es a dir, on creix i on decreix. Per tant, també queden anotats els màxims i els mínims, el domini i el recorregut.

EXEMPLE

Operacions amb funcions

A partir de funcions conegudes en podem obtenir d'altres de noves. Veurem aquí quines possibilitats tenim. Les estudiem a continuació:

Funció producte per un número
Funció suma
Funció resta
Funció producte
Funció quocient
Funció composta

Practica amb els següents exercicis:

Agència de viatges 2 .
Agència de viatges 3 .

Funció suma

També podem obtenir una nova funció sumant-ne d'altres.

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

$x$	1	2	3	4	5
$f (x)$	9	3	1	1	9

$x$	1	2	3	4	5
$g (x)$	8	9	2	7	8

Obtindrem una nova funció si sumem aquestes dues. Si la nova funció l'anomenem $h$ , podem escriure que $h = f + g$ .

I, com assignarà imatges aquesta nova funció? Doncs, la imatge segons $h$ serà la suma de les imatges segons $f$ i segons $g$ . És a dir:

h (x) = (f + g) (x) = f (x) + g (x)

Llavors, qui és $h (4)$ ?

Solució

DEFINICIÓ

Donades les funcions $f (x)$ i $g (x)$ obtindrem una nova funció sumant les dues funcions. Si la nova funció l'anomenem $h$ , podem escriure que $h = f + g$ .

I, assignarà imatges sumant les imatges de $f$ i de $g$ . És a dir:

h (x) = (f + g) (x) = f (x) + g (x)

Propietats de la suma de funcions

I si tenim les expressions algèbriques de les funcions $f$ i $g$ , com serà l'expressió algèbrica de la nova funció $h$ ?

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

f (x) =

$g (x) =$

Quina serà l'expressió algèbrica de la funció $h = f + g$ ?

Solució

I si tenim els gràfics de les funcions $f$ i $g$ , com serà el gràfic de la nova funció $h$ ?

EXEMPLE

Mou el punt etiquetat $x_{0}$ i observa la relació que hi ha entre els gràfics de les funcions $f$ , $g$ i $h$ .

RECORDA

Donades dues funcions $f (x)$ i $g (x)$ obtindrem una nova funció $h = f + g$ .
Assignarà imatges sumant les imatges de $f$ i de $g$ . És a dir: $h (x) = (f + g) (x) = f (x) + g (x)$
El domini de la nova funció $h$ seran els nombres reals que pertanyin alhora als dominis de $f$ i de $g$ . És a dir: $D_{h} = D_{f} \cap D_{g}$ .

Propietats de la suma de funcions

RECORDA

La suma de funcions té les següents propietats:

Commutativa: $f (x) + g (x) = g (x) + f (x)$
Associativa: $f (x) + [g (x) + h (x)] = [f (x) + g (x)] + h (x)$
Element neutre: existeix una funció, $o (x) = 0$ i anomenada Funció nul·la , que compleix:

$f (x) + o (x) = f (x)$
Element simètric: de qualsevol funció $f$ en tenim una altra, $- f$ i anomenada Funció oposada , que compleix:

$f (x) + [- f (x)] = o (x) = 0$

Funció nul·la

RECORDA

La funció nul·la és la que assigna a qualsevol nombre real el nombre 0. És una funció constant. La seva expressió algèbrica és $o (x) = 0$ i el seu gràfic:

Funció oposada

RECORDA

Donada una funció qualsevol $f (x)$ , la seva funció oposada (l'anomenem $- f$ ) és la que assigna a qualsevol nombre real l'oposat del que li assignava la $f$ , és adir: $(- f) (x) = - f (x)$ i el seu gràfic està relacionat amb el gràfic de la $f$ .

I si tenim l'expressió algèbrica de la funció $f$ , com serà l'expressió algèbrica de la funció oposada $- f$ ?

EXEMPLE

Donada la funció $f (x)$ .

f (x) =

Quina serà l'expressió algèbrica de la funció

- f

Solució

Practica amb el següent Exercici: Gràfic de la Funció oposada .

Funció resta

També podem obtenir una nova funció restant-ne d'altres.

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

$x$	1	2	3	4	5
$f (x)$	7	1	3	4	6

$x$	1	2	3	4	5
$g (x)$	4	2	3	8	1

Obtindrem una nova funció si restem aquestes dues. Si la nova funció l'anomenem $h$ , podem escriure que $h = f - g$ .

I, com assignarà imatges aquesta nova funció? Doncs, la imatge segons $h$ serà la resta de les imatges segons $f$ i segons $g$ . És a dir:

h (x) = (f - g) (x) = f (x) - g (x)

Llavors, qui és $h (3)$ ?

Solució

DEFINICIÓ

Donades les funcions $f (x)$ i $g (x)$ obtindrem una nova funció restant les dues funcions. Si la nova funció l'anomenem $h$ , podem escriure que $h = f - g$ .

I, assignarà imatges restant les imatges de $f$ i de $g$ . És a dir:

h (x) = (f - g) (x) = f (x) - g (x)

Restar funcions també es pot interpretar com sumar la funció oposada. És a dir:

f (x) - g (x) = f (x) + [- g (x)]

I si tenim les expressions algèbriques de les funcions $f$ i $g$ , com serà l'expressió algèbrica de la nova funció $h$ ?

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

f (x) =

$g (x) =$

Quina serà l'expressió algèbrica de la funció $h = f - g$ ?

Solució

I si tenim els gràfics de les funcions $f$ i $g$ , com serà el gràfic de la nova funció $h$ ?

EXEMPLE

Mou el punt etiquetat $x_{0}$ i observa la relació que hi ha entre els gràfics de les funcions $f$ , $g$ i $h$ .

RECORDA

Donades dues funcions $f (x)$ i $g (x)$ obtindrem una nova funció $h = f - g$ .
Assignarà imatges restant les imatges de $f$ i de $g$ . És a dir: $h (x) = (f - g) (x) = f (x) - g (x)$
El domini de la nova funció $h$ seran els nombres reals que pertanyin alhora als dominis de $f$ i de $g$ . És a dir: $D_{h} = D_{f} \cap D_{g}$ .

Funció producte

També podem obtenir una nova funció multiplicant-ne d'altres.

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

$x$	1	2	3	4	5
$f (x)$	2	5	7	1	9

$x$	1	2	3	4	5
$g (x)$	4	7	5	5	4

Obtindrem una nova funció si multipliquem aquestes dues. Si la nova funció l'anomenem $h$ , podem escriure que $h = f \cdot g$ .

I, com assignarà imatges aquesta nova funció? Doncs, la imatge segons $h$ serà la multiplicació de les imatges segons $f$ i segons $g$ . És a dir:

h (x) = (f \cdot g) (x) = f (x) \cdot g (x)

Llavors, qui és $h (1)$ ?

Solució

DEFINICIÓ

Donades les funcions $f (x)$ i $g (x)$ obtindrem una nova funció multiplicant les dues funcions. Si la nova funció l'anomenem $h$ , podem escriure que $h = f \cdot g$ .

I, assignarà imatges multiplicant les imatges de $f$ i de $g$ . És a dir:

h (x) = (f \cdot g) (x) = f (x) \cdot g (x)

Propietats del producte de funcions

I si tenim les expressions algèbriques de les funcions $f$ i $g$ , com serà l'expressió algèbrica de la nova funció $h$ ?

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

f (x) =

$g (x) =$

Quina serà l'expressió algèbrica de la funció $h = f \cdot g$ ?

Solució

I si tenim els gràfics de les funcions $f$ i $g$ , com serà el gràfic de la nova funció $h$ ?

EXEMPLE

Mou el punt etiquetat $x_{0}$ i observa la relació que hi ha entre els gràfics de les funcions $f$ , $g$ i $h$ .

RECORDA

Donades dues funcions $f (x)$ i $g (x)$ obtindrem una nova funció $h = f \cdot g$ .
Assignarà imatges multiplicant les imatges de $f$ i de $g$ . És a dir: $h (x) = (f \cdot g) (x) = f (x) \cdot g (x)$
El domini de la nova funció $h$ seran els nombres reals que pertanyin alhora als dominis de $f$ i de $g$ . És a dir: $D_{h} = D_{f} \cap D_{g}$ .

Propietats del producte de funcions

RECORDA

El producte de funcions té les següents propietats:

Commutativa: $f (x) \cdot g (x) = g (x) \cdot f (x)$
Associativa: $f (x) \cdot [g (x) \cdot h (x)] = [f (x) \cdot g (x)] \cdot h (x)$
Element neutre: existeix una funció, $u (x) = 1$ i anomenada Funció unitat , que compleix:

$f (x) \cdot u (x) = f (x)$
Element simètric: de qualsevol funció $f$ en tenim una altra, $\frac{1}{f}$ i anomenada Funció recíproca , que compleix:

$f (x) \cdot (\frac{1}{f}) (x) = u (x) = 1$

Funció unitat

RECORDA

La funció unitat és la que assigna a qualsevol nombre real el nombre 1. És una funció constant. La seva expressió algèbrica és $u (x) = 1$ i el seu gràfic:

Funció recíproca

RECORDA

Donada una funció qualsevol $f (x)$ , la seva funció recíproca (l'anomenem $\frac{1}{f}$ ) és la que assigna a qualsevol nombre real l'invers del que li assignava la $f$ , és adir: $(\frac{1}{f})$ (x) $= \frac{1}{f (x)}$ i el seu gràfic està relacionat amb el gràfic de la $f$ .

I si tenim l'expressió algèbrica de la funció $f$ , com serà l'expressió algèbrica de la funció recíproca $\frac{1}{f}$ ?

EXEMPLE

Donada la funció $f (x)$ .

f (x) =

Quina serà l'expressió algèbrica de la funció

\frac{1}{f}

Solució

Funció quocient

També podem obtenir una nova funció dividint-ne d'altres.

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

$x$	1	2	3	4	5
$f (x)$	6	2	9	3	7

$x$	1	2	3	4	5
$g (x)$	4	1	4	5	7

Obtindrem una nova funció si dividim aquestes dues. Si la nova funció l'anomenem $h$ , podem escriure que $h = \frac{f}{g}$ .

I, com assignarà imatges aquesta nova funció? Doncs, la imatge segons $h$ serà la divisió de les imatges segons $f$ i segons $g$ . És a dir:

h (x) = (\frac{f}{g}) (x) = \frac{f (x)}{g (x)}

Llavors, qui és $h (3)$ ?

Solució

DEFINICIÓ

Donades les funcions $f (x)$ i $g (x)$ obtindrem una nova funció dividint les dues funcions. Si la nova funció l'anomenem $h$ , podem escriure que $h = \frac{f}{g}$ .

I, assignarà imatges dividint les imatges de $f$ i de $g$ . És a dir:

h (x) = (\frac{f}{g}) (x) = \frac{f (x)}{g (x)}

I si tenim les expressions algèbriques de les funcions $f$ i $g$ , com serà l'expressió algèbrica de la nova funció $h$ ?

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

f (x) =

$g (x) =$

Quina serà l'expressió algèbrica de la funció $h = \frac{f}{g}$ ?

Solució

I si tenim els gràfics de les funcions $f$ i $g$ , com serà el gràfic de la nova funció $h$ ?

EXEMPLE

Mou el punt etiquetat $x_{0}$ i observa la relació que hi ha entre els gràfics de les funcions $f$ , $g$ i $h$ .

Fixa't en el domini de la nova funció $h$ .

RECORDA

Donades dues funcions $f (x)$ i $g (x)$ obtindrem una nova funció $h = \frac{f}{g}$ .
Assignarà imatges dividint les imatges de $f$ i de $g$ . És a dir: $h (x) = (\frac{f}{g}) (x) = \frac{f (x)}{g (x)}$
El domini de la nova funció $h$ seran els nombres reals que pertanyin alhora als dominis de $f$ i de $g$ i que no anul·lin el denominador. És a dir: $D_{h} = D_{f} \cap D_{g} \cap {x \in ℝ / g (x) \neq 0}$ .

Per entendre millor el tema del domini de la nova funció quocient fixa't en el següent exemple.

EXEMPLE

Fixa't en el domini de les noves funcions $h$ i $j$ .

Funció composta

Una altra possibilitat d'obtenir una nova funció a partir d'altres és fer-les actuar una darrera de l'altra.

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

$x$	1	2	3	4	5
$f (x)$	5	4	3	2	4

$x$	1	2	3	4	5
$g (x)$	8	8	5	9	6

Obtindrem una nova funció si fem actuar primer, per exemple, la funció $f$ i sobre el que obtenim fem actuar llavors la funció $g$ . D'aquesta manera d'obtenir noves funcions en diem composició de funcions, i el símbol que utilitzem és $\circ$ . Si la nova funció l'anomenem $h$ , podem escriure que $h = g \circ f$ .

Fixa't que hem posat les funcions en l'ordre invers a com actuen. Com pots intuir, i després veurem, en aques cas l'ordre és impostant.

I, com assignarà imatges aquesta nova funció? Doncs, la imatge segons $h$ serà la imatge segons $g$ de la imatge segons $f$ . És a dir:

h (x) = (g \circ f) (x) = g (f (x))

Llavors, qui és $h (1)$ ?

Solució

DEFINICIÓ

Donades les funcions $f (x)$ i $g (x)$ obtindrem una nova funció si fem actuar primer, per exemple, la funció $f$ i sobre el que obtenim fem actuar llavors la funció $g$ . Si la nova funció l'anomenem $h$ , podem escriure que $h = g \circ f$ . I diem que és la funció composta.

La imatge segons $h$ serà la imatge segons $g$ de la imatge segons $f$ . És a dir:

h (x) = (g \circ f) (x) = g (f (x))

Propietats de la composició de funcions

I si tenim les expressions algèbriques de les funcions $f$ i $g$ , com serà l'expressió algèbrica de la nova funció $h$ ? Anem a veure-ho amb uns exemples.

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

f (x) =

$g (x) =$

Quina serà l'expressió algèbrica de les funcions:

$h_{1} = f \circ g$
$h_{2} = g \circ f$

Solució

I si tenim els gràfics de les funcions $f$ i $g$ , com serà el gràfic de la nova funció $h$ ? Doncs en aquest cas les situacions són molt diverses i veurem aquí les més interessants en els següents exemples:

Translacions
Reflexions
Amb valor absolut
Deformacions

RECORDA

Donades dues funcions $f (x)$ i $g (x)$ obtindrem una nova funció $h = g \circ f$ . És la funció composta.
La imatge segons $h$ serà la imatge segons $g$ de la imatge segons $f$ . És a dir: $h (x) = (g \circ f) (x) = g (f (x))$ .

El domini de la funció composta és un tema delicat. Fixa't en el següent exemple.

EXEMPLE

Donades les funcions $f (x)$ i $g (x)$ .

f (x) = x^{2} - 4

$g (x) = \sqrt{4 - x^{2}}$

Si obtenim l'expressió algèbrica de la funció $h = f \circ g$ :

h (x) = (f \circ g) (x) =

f (g (x)) = f (\sqrt{4 - x^{2}}) = {(\sqrt{4 - x^{2}})}^{2} - 4 = 4 - x^{2} - 4 = - x^{2}

Si mirem aquesta darrera expressió algèbrica podríem pensar que el domini de la funció

h

són tots el nombres reals. Però això no és correcte. En aquest cas el domini de

h

coincideix amb el de

g

. Així que hauríem d'escriure:

h (x) = - x^{2}, D_{h} = [- 2, 2]

Que, d'alguna manera, vol dir: pots utilitzar l'expressió

- x^{2}

per calcular imatges per la funció

h

, però només si els

x \in [- 2, 2]

. Els altres no tenen imatge per la funció

h

. Pots veure-ho en el següent gràfic:

Propietats de la composició de funcions

RECORDA

La composició de funcions té les següents propietats:

Associativa: $[f \circ (g \circ h)] (x) = [(f \circ g) \circ h] (x)$

Element neutre: existeix una funció, $I (x) = x$ i anomenada Funció identitat , que compleix: $(f \circ I) (x) = f (x)$ $(I \circ f) (x) = f (x)$

Element simètric: de qualsevol funció $f$ en tenim una altra, $f^{- 1}$ i anomenada Funció inversa , que compleix:

$(f \circ f^{- 1}) (x) = I (x) = x$ $(f^{- 1} \circ f) (x) = I (x) = x$

Destacar que, com s'ha vist en algun exemple anteriorment, la composició de funcions no té la propietat commutativa. És a dir:

f \circ g \neq g \circ f

Això vol dir que $f \circ g$ i $g \circ f$ no sempre coincideixen.

Translacions

Si una de les funcions que intervenen en la composició és

f (x) = x + k

, on

k \in ℝ

, la nova funció

h

és una transformació de la funció

g

. Ho veurem amb uns exemples:

EXEMPLE

Observa que quan una de les funcions que intervenen en la composició és $f (x) = x + k$ i actua en segon lloc, la nova funció $h (x) = (f \circ g) (x) = f (g (x)) = g (x) + k$ té un gràfic que és una translació vertical cap a dalt si $k > 0$ i cap a baix si $k < 0$ .

És a dir, el gràfic de la funció $h (x) = (f \circ g) (x) = f (g (x)) = g (x) + k$ el podem obtenir a partir del de $g$ fent una translació de vector $\overset{⇀}{v} = (0, k)$ .

EXEMPLE

Ara s'ha canviat l'ordre de les funcions que intervenen en la composició, la funció $f (x) = x + k$ actua en primer lloc, la nova funció $h (x) = (g \circ f) (x) = g (f (x)) = g (x + k)$ té un gràfic que és una translació horitzontal cap a l'esquerra si $k > 0$ i cap a la dreta si $k < 0$ .

És a dir, el gràfic de la funció $h (x) = (g \circ f) (x) = g (f (x)) = g (x + k)$ el podem obtenir a partir del de $g$ fent una translació de vector $\overset{⇀}{v} = (- k, 0)$ .

RECORDA

Si tenim una funció qualsevol $g (x)$ i una altra $f (x) = x + k$ , on $k \in ℝ$ :

El gràfic d'una funció $h (x) = (f \circ g) (x) = f (g (x)) = g (x) + k$ el podrem obtenir fent una translació vertical cap:
- amunt si $k > 0$ de $k$ unitats.
- avall si $k < 0$ de $k$ unitats.
El gràfic d'una funció $h (x) = (g \circ f) (x) = g (f (x)) = g (x + k)$ el podrem obtenir fent una translació horitzontalal cap:
- a l'esquerra si $k > 0$ de $k$ unitats.
- a la dreta si $k < 0$ de $k$ unitats.

També podem trobar-nos el cas d'una composició de més de dues funcions. Suposem que tenim una funció qualsevol $g (x)$ , una altra $f (x) = x + k$ i una altra $h (x) = x + m$ , on $k, m \in ℝ$ . És interessant el cas en el que les funcions $f$ i $h$ actuen una al davant i l'altra al darrere de la funció $g$ (dit d'una altra manera, la $g$ actua al mig). Mira l'exemple:

EXEMPLE

Observa que en aquesta situació el gràfic de la nova funció $j = f \circ g \circ h$ sent $g$ una funció qualsevol i $f (x) = x + k$ i $h (x) = x + m$ , on $k, m \in ℝ$ és el resultat de dues translacions, una horitzontal i l'altra vertical, del gràfic de la funció $g$ .

És a dir, el gràfic de la funció $j (x) = (f \circ g \circ h) (x) = g (x + m) + k$ el podem obtenir a partir del de $g$ fent una translació de vector $\overset{⇀}{v} = (- m, k)$ .

Reflexions

Un cas també interessant es produeix quan una de les funcions que intervenen en la composició és

f (x) = - x

, la nova funció

h

és una transformació de la funció

g

. Ho veurem amb uns exemples:

EXEMPLE

Observa que quan una de les funcions que intervenen en la composició és $f (x) = - x$ i actua en segon lloc, la nova funció $h (x) = (f \circ g) (x) = f (g (x)) = - g (x)$ té un gràfic que és una reflexió vertical del gràfic de la funció $g$ .

És a dir, el gràfic de la funció $h (x) = (f \circ g) (x) = f (g (x)) = - g (x)$ el podem obtenir a partir del de $g$ fent una reflexió respecte l'eix OX.

EXEMPLE

Ara s'ha canviat l'ordre de les funcions que intervenen en la composició, la funció $f (x) = - x$ actua en primer lloc, la nova funció $h (x) = (f \circ g) (x) = f (g (x)) = g (- x)$ té un gràfic que és una reflexió horitzontal del gràfic de la funció $g$ .

És a dir, el gràfic de la funció $h (x) = (g \circ f) (x) = g (f (x)) = g (- x)$ el podem obtenir a partir del de $g$ fent una reflexió respecte l'eix OY.

RECORDA

Si tenim una funció qualsevol $g (x)$ i una altra $f (x) = - x$ :

El gràfic d'una funció $h (x) = (f \circ g) (x) = f (g (x)) = - g (x)$ el podem obtenir a partir del de $g$ fent una reflexió respecte l'eix OX.
El gràfic d'una funció $h (x) = (g \circ f) (x) = g (f (x)) = g (- x)$ el podem obtenir a partir del de $g$ fent una reflexió respecte l'eix OY.

També podem trobar-nos el cas d'una composició de més de dues funcions. Suposem que tenim una funció qualsevol $g (x)$ , una altra $f (x) = - x$ i una altra $h (x) = x + m$ , on $m \in ℝ$ . És interessant el cas en el que les funcions $f$ i $h$ actuen una al davant i l'altra al darrere de la funció $g$ (dit d'una altra manera, la $g$ actua al mig). Mira l'exemple:

EXEMPLE

Observa que en aquesta situació el gràfic de la nova funció $j = f \circ g \circ h$ sent $g$ una funció qualsevol i $f (x) = - x$ i $h (x) = x + m$ , on $m \in ℝ$ és el resultat de dues transformacions, una translació horitzontal i una reflexió vertical, del gràfic de la funció $g$ .

És a dir, el gràfic de la funció $j (x) = (f \circ g \circ h) (x) = - g (x + m)$ el podem obtenir a partir del de $g$ fent una translació horitzontal i una reflexió vertical del gràfic de la funció $g$ .

Amb valor absolut

Un altre cas també interessant es produeix quan una de les funcions que intervenen en la composició és

f (x) = ∣ x ∣

, la nova funció

h

és una transformació de la funció

g

. Ho veurem amb uns exemples:

EXEMPLE

Observa que quan una de les funcions que intervenen en la composició és $f (x) = ∣ x ∣$ i actua en segon lloc, la nova funció $h (x) = (f \circ g) (x) = f (g (x)) = ∣ g (x)$ | té un gràfic que coincideix amb el de $g$ per sobre de l'eix OX i la part del gràfic de $g$ que està per sota de l'eix OX la reflecteix simètricament per sobre.

EXEMPLE

Ara s'ha canviat l'ordre de les funcions que intervenen en la composició, la funció $f (x) = ∣ x ∣$ actua en primer lloc, la nova funció $h (x) = (f \circ g) (x) = f (g (x)) = g (∣ x ∣)$ té un gràfic que coincideix amb el de $g$ a la dreta de l'eix OY i la part del gràfic de $g$ que està a la dreta de l'eix OY la reflecteix simètricament a l'esquerra.

RECORDA

Si tenim una funció qualsevol $g (x)$ i una altra $f (x) = ∣ x ∣$ :

El gràfic d'una funció $h (x) = (f \circ g) (x) = f (g (x)) = ∣ g (x) ∣$ coincideix amb el de $g$ per sobre de l'eix OX i la part del gràfic de $g$ que està per sota de l'eix OX la reflecteix simètricament per sobre.
El gràfic d'una funció $h (x) = (g \circ f) (x) = g (f (x)) = g (∣ x ∣)$ coincideix amb el de $g$ a la dreta de l'eix OY i la part del gràfic de $g$ que està a la dreta de l'eix OY la reflecteix simètricament a l'esquerra.

També podem trobar-nos el cas d'una composició de més de dues funcions. Suposem que tenim una funció qualsevol $g (x)$ , una altra $f (x) = ∣ x ∣$ i una altra $h (x) = x + m$ , on $m \in ℝ$ . És interessant el cas en el que les funcions $f$ i $h$ actuen una al davant i l'altra al darrere de la funció $g$ (dit d'una altra manera, la $g$ actua al mig). Mira l'exemple:

EXEMPLE

Observa que en aquesta situació el gràfic de la nova funció $j = f \circ g \circ h$ sent $g$ una funció qualsevol i $f (x) = ∣ x ∣$ i $h (x) = x + m$ , on $m \in ℝ$ és el resultat de dues transformacions, una translació horitzontal i una còpia simètrica del que està per sota de l'eix OX cap a dalt de l'eix OX, del gràfic de la funció $g$ .

És a dir, el gràfic de la funció $j (x) = (f \circ g \circ h) (x) = ∣ g (x + m) ∣$ el podem obtenir a partir del de $g$ fent una translació horitzontal i una còpia simètrica del que està per sota de l'eix OX cap a dalt de l'eix OX, del gràfic de la funció $g$ .

Deformacions

Si una de les funcions que intervenen en la composició és

f (x) = k x

, on

k \in ℝ, k > 0

, la nova funció

h

és una transformació de la funció

g

. Ho veurem amb uns exemples:

EXEMPLE

Observa que quan una de les funcions que intervenen en la composició és $f (x) = k x$ i actua en segon lloc, la nova funció $h (x) = (f \circ g) (x) = f (g (x)) = k g (x)$ té un gràfic que és una dilatació vertical si $k > 1$ o una contracció vertical si $k < 1$ .

És a dir, el gràfic de la funció $h (x) = (f \circ g) (x) = f (g (x)) = k g (x)$ el podem obtenir a partir del de $g$ fent una dilatació vertical si $k > 1$ o una contracció vertical si $k < 1$ .

EXEMPLE

Ara s'ha canviat l'ordre de les funcions que intervenen en la composició, la funció $f (x) = k x$ actua en primer lloc, la nova funció $h (x) = (g \circ f) (x) = g (f (x)) = g (k x)$ té un gràfic que és una contracció horitzontal si $k > 1$ o una dilatació horitzontal si $k < 1$ .

És a dir, el gràfic de la funció $h (x) = (g \circ f) (x) = g (f (x)) = g (k x)$ el podem obtenir a partir del de $g$ fent una contracció horitzontal si $k > 1$ o una dilatació horitzontal si $k < 1$ .

RECORDA

Si tenim una funció qualsevol $g (x)$ i una altra $f (x) = x + k$ , on $k \in ℝ$ :

El gràfic d'una funció $h (x) = (f \circ g) (x) = f (g (x)) = k g (x)$ el podrem obtenir a partir del de $g$ fent una:
- dilatació vertical si $k > 1$ de factor $k$ .
- contracció vertical si $k < 1$ de factor $k$ .
El gràfic d'una funció $h (x) = (g \circ f) (x) = g (f (x)) = g (k x)$ el podrem obtenir a partir del de $g$ fent una:
- contracció horitzontal si $k > 1$ de factor $k$ .
- dilatació horitzontal si $k < 1$ de factor $k$ .

També podem trobar-nos el cas d'una composició de més de dues funcions. Suposem que tenim una funció qualsevol $g (x)$ , una altra $f (x) = k x$ i una altra $h (x) = x + m$ , on $k, m \in ℝ, k > 0$ . És interessant el cas en el que les funcions $f$ i $h$ actuen una al davant i l'altra al darrere de la funció $g$ (dit d'una altra manera, la $g$ actua al mig). Mira l'exemple:

EXEMPLE

Observa que en aquesta situació el gràfic de la nova funció $j = f \circ g \circ h$ sent $g$ una funció qualsevol i $f (x) = k x$ i $h (x) = x + m$ , on $k, m \in ℝ, k > 0$ és el resultat d'una translació horitzontal i una contracció o dilatació vertical segons el valor de $k$ , del gràfic de la funció $g$ .

És a dir, el gràfic de la funció $j (x) = (f \circ g \circ h) (x) = k g (x + m)$ el podem obtenir a partir del de $g$ fent una translació horitzontal i una contracció o dilatació vertical segons el valor de $k$ .

Funció producte per un número

Multiplicant una funció per un nombre real obtenim una nova funció.

EXEMPLE

Donada la funció $f (x)$ .

$x$	1	2	3	4	5
$f (x)$	3	4	7	8	8

Obtindrem una nova funció si la multipliquem per un número, per exemple per 4. Si la nova funció l'anomenem $g$ , podem escriure que $g = 4 \cdot f$ .

I, com assignarà imatges aquesta nova funció? Doncs, la imatge segons $g$ serà la imatge segons $f$ multiplicada per 4. És a dir:

g (x) = (4 \cdot f) (x) = 4 \cdot f (x)

Llavors, qui és $g (2)$ ?

Solució

DEFINICIÓ

Donada una funció $f (x)$ i un $k \in ℝ$ obtindrem una nova funció multiplicant la funció $f (x)$ pel número $k$ . Si la nova funció l'anomenem $g$ , podem escriure que $g = k \cdot f$ .

I, assignarà imatges multiplicant per $k$ les imatges de $f$ . És a dir:

g (x) = (k \cdot f) (x) = k \cdot f (x)

I si tenim l'expressió algèbrica de la funció $f$ , com serà l'expressió algèbrica de la nova funció $g$ ?

EXEMPLE

Donada la funció $f (x)$ .

f (x) =

Quina serà l'expressió algèbrica de la funció $g = 3 \cdot f$ ?

Solució

I si tenim el gràfic de la funció $f$ , com serà el gràfic de la nova funció $g$ ?

EXEMPLE

Modifica el valor de k i mou el punt blau i observa la relació que hi ha entre els gràfics de les funcions $f$ i $g$ .

RECORDA

Donada una funció $f (x)$ i un $k \in ℝ$ obtindrem una nova funció $g = k \cdot f$ .
Assignarà imatges multiplicant per $k$ les imatges de $f$ . És a dir: $g (x) = (k \cdot f) (x) = k \cdot f (x)$
El domini de la nova funció $g$ serà el mateix que el de la funció $f$ . És a dir: $D_{g} = D_{f}$ .

Funció inversa

Donada una funció

f

, la funció inversa de

f

és una altra funció, que representem per

f^{- 1}

, que desfà l'acció que ha fet

f

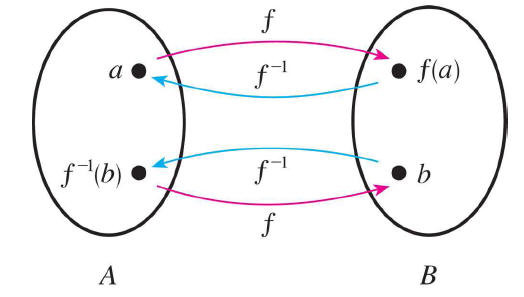
Per exemple, si tenim una funció $f$ que al 3 li assigna el 8, la seva funció inversa $f^{- 1}$ al 8 li assignarà el 3, Dit d'una altra manera, si la funció $f$ passa pel punt $(3, 8)$ , la seva funció inversa $f^{- 1}$ passarà pel punt $(8, 3)$ .

També, si tenim una funció $f$ que assigna imatges multiplicant per 3, és a dir, $f (x) = 3 x$ , la seva funció inversa $f^{- 1}$ assignarà imatges dividint per 3, és a dir, $f^{- 1} (x) = \frac{x}{3}$ .

Concretant, això vol dir que si la imatge de 5 per $f$ és 15, la imatge de 15 per $f^{- 1}$ ha de ser 5. Expressant-ho formalment:

f (5) = 3 \cdot 5 = 15

f^{- 1} (15) = \frac{15}{3} = 5

Dit d'una altra manera, quan actua una funció darrera de l'altra (recorda: això és una composició de funcions) sobre el 5 obtenim el mateix 5.

(f^{- 1} \circ f) (5) = f^{- 1} (f (5)) = f^{- 1} (15) = 5

També:

(f \circ f^{- 1}) (15) = f (f^{- 1} (15)) = f (5) = 15

I això s'ha de complir no només per al 5 sinó per a qualsevol nombre real $x \in ℝ$ .

(f^{- 1} \circ f) (x) = f^{- 1} (f (x)) = f^{- 1} (3 x) = \frac{3 x}{3} = x

També:

(f \circ f^{- 1}) (x) = f (f^{- 1} (x)) = f (\frac{x}{3}) = 3 \cdot \frac{x}{3} = x

DEFINICIÓ

Diem que una funció $f^{- 1}$ és la inversa d'una altra $f$ quan es compleixen:

$(f^{- 1} \circ f) (x) = x$
$(f \circ f^{- 1}) (x) = x$

Cal tenir en compte que hi ha funcions que no tenen inversa. I que si una funció $f$ té inversa, la inversa d'aquesta inversa és la mateixa $f$ . Ès a dir: ${(f^{- 1})}^{- 1} = f$ .

Càlcul de la funció inversa
Gràfic de la funció inversa
Quines funcions no tenen inversa?

Càlcul de la funció inversa

En els casos més senzills podem trobar la funció inversa directament.

EXEMPLE

Troba la funció inversa de $f (x) = 6 x$ . Després comprova que $(f^{- 1} \circ f) (x) = x$ i $(f \circ f^{- 1}) (x) = x$ .

Solució

Exercici: Càlcul de la funció inversa - I

Pot ser que ens interessi comprovar si una funció és inversa d'una altra.

EXEMPLE

Quina de les funcions $g (x)$ o $h (x)$ és la funció inversa de $f (x) = \frac{4}{x - 6}$ .

g (x) = \frac{x - 6}{4} h (x) = \frac{4}{x} + 6

Solució

Quan l'expressió de la funció $f$ és més complexa, no és tan fàcil trobar l'expressió de la inversa. En aquests casos podem seguir els següents passos:

Igualar l'expressió de la funció $f (x)$ a $y$ .
Aïllar la $x$ a la igualtat anterior.
Canviar $x$ per $y$ i viceversa.

EXEMPLE

Troba la inversa de la funció $f (x) = \frac{}{}$ .

Solució

Si ens demanen que després de trobar la funció inversa comprovem que ho és, hem de comprovar, tal com hem fet als dos primers exemples, que:

(f^{- 1} \circ f) (x) = x

(f \circ f^{- 1}) (x) = x

Gràfic de la funció inversa

Ara ens interessa veure quina relació hi ha entre el gràfic d'aquestes dues funcions,

f

f^{- 1}

. Començarem recordant que si

f

passa pel punt

(5, 15)

, llavors

f^{- 1}

passa pel punt

(15, 5)

. És a dir, el punt amb les mateixes coordenades però canviades d'ordre. I això què suposarà pel que fa al gràfic?

En el gràfic següent s'ha construït un punt B amb les mateixes coordenades que un altre A però canviades de lloc. Mou el punt blau A i te n'adonaràs quina relació hi ha.

Així, doncs, podem dir que els gràfics de les funcions $f$ i $f^{- 1}$ són simètrics respecte de la bisectriu del primer i tercer quadrants (la recta d'equació $y = x$ ).

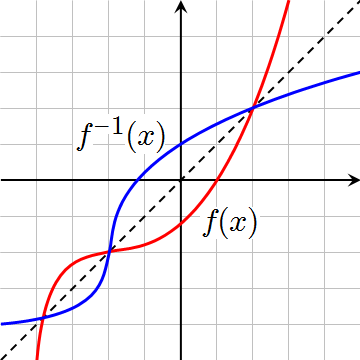
Quines funcions no tenen inversa?

Ja hem dit que no totes les funcions tenen inversa. Però, quines són les que no en tenen?

Doncs aquelles que tenen algun/s valor/s de la variable dependent amb més d'una antiimatge. Perquè la seva inversa assignaria a aquest valor més d'una imatge i recordem que les funcions a cada valor de la variable independent els hi assignen un ÚNIC valor de la variable dependent.

Això ho podem veure en qualsevol de les formes en que pot venir donada una funció. En forma de taula.

$x$	-1	2	3	5	8	9
$f (x)$	3	-5	1	3	2	0

Observa que el 3 té dues antiimatges, el -1 i el 5. Llavors $f^{- 1}$ li assignaria, al 3, dues imatges i per tant no seria funció. Diem que $f$ no té inversa, $∄ f^{- 1}$ . El mateix passa en les següents situacions:

$g (x) = {(1, 9), (2, 13), (3, 15), (4, 15), (5, 12), (6, 10)}$
$∄ g^{- 1}$	$∄ h^{- 1}$

Són especialment interessants els casos en que la funció ens la donen en forma de gràfic o de fórmula. Els analitzem conjuntament.

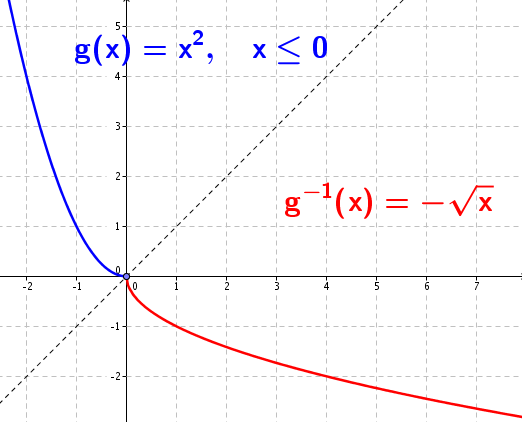
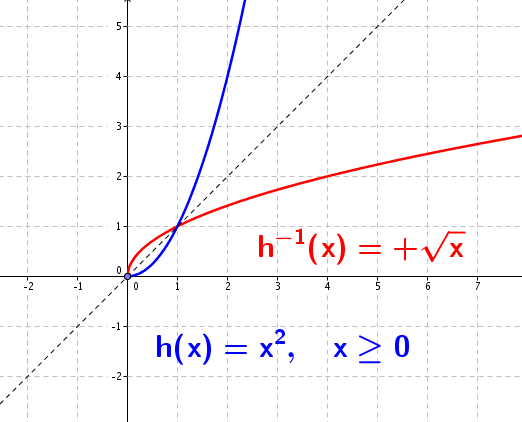
Donada la funció $f (x) = x^{2}$ . En intentar trobar la inversa fem: $y = x^{2} \to x = \pm \sqrt{y} \to y = \pm \sqrt{x}$ i això ja ens indica que $∄ f^{- 1}$ , qualsevol $x \in ℝ^{+}$ tindria dues imatges i això no pot ser.

Analitzem-ho ara gràficament. Saps molt bé que el gràfic de la funció $f (x) = x^{2}$ és la paràbola següent, i el gràfic de la inversa hauria de ser el que veus, però ... clar, no seria funció!!

La idea és la següent: si es pot dibuixar alguna línia recta horitzontal que talli el gràfic de la funció $f$ en més d'un punt, llavors la funció $f$ no té inversa. És a dir, $∄ f^{- 1}$ .

Dit d'una altra manera, si totes les línies rectes horitzontals que es poden dibuixar tallen el gràfic de la funció $f$ com a màxim en un punt, llavors la funció $f$ té inversa. És a dir, $\exists f^{- 1}$ .

Però les funcions que no tenen inversa podem desfer-les en trossos de manera adequada per tal que en cada tros sí que tinguin inversa. I, com ho fem això de fer trossos d'una funció? Doncs, restringint el domini. Agafant una part només del domini inicial de la funció. És per això que aquestes inverses s'anomenen inversa parcial o inversa local .

En el cas de la funció anterior $f (x) = x^{2}$ faríem el següent:


$\exists g^{- 1}$	$\exists h^{- 1}$

Concepte de funció.
Domini i recorregut d'una funció
Funcions algèbriques
Funcions definides a trossos
Taula de variació d'una funció
Operacions amb funcions
Funció inversa

funcions i operacions amb funcions.
: , interactive mathematics, interactive math, server side interactivity

The most recent version